Robust and Efficient Adaptive Direct Lighting Estimation

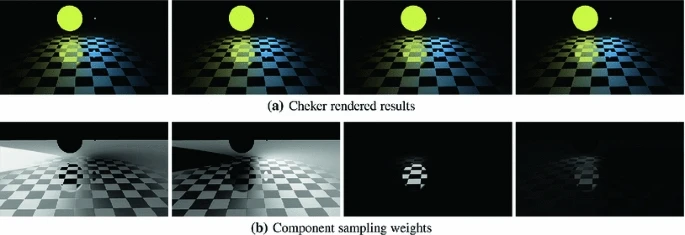
Hemispherical integral is important for the estimation of direct lighting which has major impact on the results of global illumination. This work first proposes the population Monte Carlo hemispherical integral (PMC-HI) sampler to improve the efficiency of hemispherical integral estimation. The sampler is unbiased and derived from the population Monte Carlo framework. The hemispherical integral sampler works on a population of samples and learns to be a better sampling function over iterations. Information found in one iteration can be used to guide subsequent iterations by distributing more samples to important sampling techniques such as sampling from light and sampling from BSDF in order to focus more efforts on the sampling sub-domain which has larger contribution to the integral. In addition, a cone sampling is proposed based on the previous successful sampling results to enhance the success rate when complex occlusions exist. In addition, we also adapt the image-plane multidimensional adaptive sampling proposed by Hachisuka et al. [15] for multidimensional hemi spherical adaptive sampling (MDHI) to estimate the hemispherical integrals deterministically in the random-number direct lighting space. The images rendered with PMC-HI and MDHI are compared against those rendered with multiple importance sampling (MIS) [30] and adaptive light sample distributions (ALSD) [6]. Our PMC-HI sampler can significantly improve the rendering efficiency. Furthermore, we also show that PMC-HI can be implemented as a plugin to a modern global rendering system.